Prime Factorization Of 2025 A Comprehensive Exploration
In this auspicious occasion, we are delighted to delve into the intriguing topic related to Prime Factorization of 2025: A Comprehensive Exploration. Let’s weave interesting information and offer fresh perspectives to the readers.


Prime factorization, a fundamental concept in number theory, involves expressing a composite number as a product of its prime factors. Prime factors are prime numbers that cannot be further broken down into smaller integers. Understanding prime factorization is crucial for solving various mathematical problems and has applications in cryptography, computer science, and other fields.

In this article, we delve into the prime factorization of 2025, a composite number. We will employ different methods to find its prime factors and explore the significance of prime factorization in understanding the properties and behavior of numbers.

Trial division is a straightforward method for finding the prime factors of a number. It involves repeatedly dividing the number by the smallest prime number that divides it evenly until the result is 1.

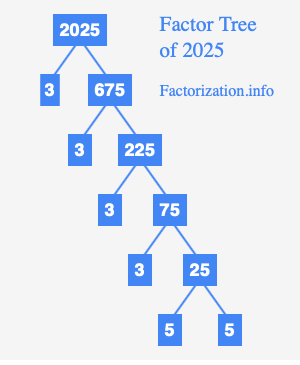
A factor tree is a graphical representation of the prime factorization of a number. It starts with the number at the top and branches out into its prime factors.

For certain numbers, it is possible to find their prime factors using a formula. For example, if a number is of the form n = p^a × q^b, where p and q are distinct prime numbers and a and b are positive integers, then the prime factorization is:
Unique Representation: Every composite number has a unique prime factorization, which is independent of the method used to find it. This unique representation allows us to identify and compare numbers based on their prime factors.

Divisibility: The prime factors of a number determine its divisors. For instance, if a number has a prime factor of 2, it is divisible by 2.

Greatest Common Factor (GCF) and Least Common Multiple (LCM): The GCF of two numbers is the product of their common prime factors, while the LCM is the product of all their prime factors. Prime factorization helps in finding the GCF and LCM efficiently.
Number Theory Applications: Prime factorization plays a crucial role in number theory, particularly in areas such as modular arithmetic, Diophantine equations, and cryptography.
The prime factorization of 2025, as determined by the methods discussed above, is 2025 = 3 × 3 × 3 × 5 × 5. Prime factorization provides valuable insights into the structure and properties of numbers. It is a fundamental concept with applications in various mathematical and scientific fields. Understanding prime factorization enhances our ability to solve problems, explore number theory, and appreciate the intricate nature of numbers.







Thus, we hope this article has provided valuable insights into Prime Factorization of 2025: A Comprehensive Exploration. We thank you for taking the time to read this article. See you in our next article!